julia, using SymPy で、センター試験の2次関数に挑む
【センター試験 2006年度:数学I・A(本試験) 第2問】というやつに、SymPy を呼び出した julia で挑んでみます。なぜ、2006年度かというと、google 先生が、"センター試験 数学 I 2次関数" で、1番目にお示しになったからです。
準備
インストール済みの方は不要です。
Pkg.add("PyCall")
Pkg.add("SymPy")
Pkg.add("Plots")
前半
y=6x^2+11x-10 について、y≦0となるxの値の範囲が、1問目です。下に凸なので、y=0 とした時の解の間です (残念ながら、すべて自動では無理だと思います) 。
using Plots, PyCall, SymPy # (注) 2017年6月5日現在、Plots しか下記の方法だと動かないようです。 @syms x y f= 6x^2+11x-10 solve(f)
で、y=0 の時が解けます。
julia> solve(f)
2-element Array{SymPy.Sym,1}:
-5/2
2/3
plot(f) で確認で、グラフでも確認。y<=0 のときは、-5/2 <= x <= 2/3 で良いでしょう。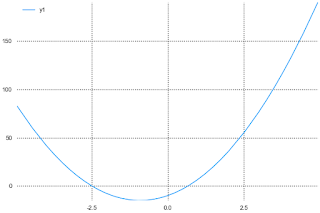
続いてx, y 方向それぞれ a, b だけ平行移動して、この曲線が、原点 (0,0) を通るようにするようです。(x,y) に (x-a , y-b) を代入します。誘導を見ると、まず、x=0, y=0 とした時の b を、a で表すことになります。つまり、x=-a, y=-b として、b について解きます。y=-b なので、右辺にー1を掛けて、x=-a を代入すれば良いです。
を入力して、@syms a b b =-subs(f, (x,-a))
julia> b =-subs(f, (x,-a))
2
- 6⋅a + 11⋅a + 10
この b の値を使って、f(x)= 6x^2+11x-10 とした際の y-b = f(x-a) を、y について解く、つまり、y = f(x-a) + b の右辺を計算します。
として、y = subs(f, (x, x-a)) +b # f(x-a) + b y = expand(y) # 展開 y = collect(y, x) # x について整理
julia> y = collect(y, x) 2 6⋅x + x⋅(-12⋅a + 11)
これが式(2) となります。これで前半終了です。
後半
説明のため(2)式を g(x) = 6⋅x^2 + x⋅(-12a + 11) としましょう。
x=−2と x=3 で値が同じとのことですから、g(-2) = g(3) つまり、g(-2)-g(3) = 0 で、a の値を求めましょう。solve( subs(y, (x,-2)) - subs(y, (x, 3))) で、変数は a だけになりますので、a の値が求まります。
julia> solve( subs(y, (x,-2)) - subs(y, (x, 3)))
1-element Array{SymPy.Sym,1}:
17/12
したがって、a =17/12
これを式(2) に代入します。
julia> y2 = subs(y, (a, 17//12)) # 検算の時に y を上書きすると困るので、便宜的に y2 とします。17//12 とするとこの後が整数もなります。
2
⎛ 17⎞ 289
11⋅x + 6⋅⎜x - ──⎟ - ───
⎝ 12⎠ 24
julia> y2 = expand(y2)
2
6⋅x - 6⋅x
次に、y = 6x^2 - 6x について −2≦x≦3 で最小値と最大値を求めます。
2次関数ですから、まず、頂点の座標を求めましょう。本来なら平方完成です。ところが、平方完成は、SymPy では、かえって難しそうですので、ちょっとズルをして、yをxについて微分して0になるxの値をもって、頂点の座標としてしまいます。
julia> solve(diff(y2))
1-element Array{SymPy.Sym,1}:
1/2
したがって、x=1/2 で頂点です。なんと、-2 と 3 の中間点ですね。この時のyの値は、y2(1//2) = -3/2 つまり、頂点の座標は、(1/2, -3/2) です。ー2 < 1/2 < 3 で、グラフは下に凸です。したがって、頂点は、ー2 <= x <= 3 の間にありますね。したがって頂点が最小で、yの最小値は、-3/2 です。
ここで、ちょっと上を見て、x=−2とx=3に対応する2次関数 (2) が、等しくなるように、苦労してきたことを思い出してみましょう。つまり、ー2 <= x <= 3 における y の値は、x=-2 でも x=3 でも等しくなり、これが最大値です。では、両方代入して、等しいことも一緒に確認しましょう。
julia> y2(-2) # subs(y, (x,-2)) と同じ。変数がひとつなら、y(x) の方が文字数が少ないですね。 36 julia> y2(3) 36
以上、最大値は、36 でした。
確認の意味で、plot(y2)
結構、大きな値まで出てくるグラフなので、頂点近傍は、見にくいですね。放物線のところは、確実に計算すればできますが、計算量が多くて、苦手に感じている人も多いと思います。a =17/12 なんて、大きな数字の分数を見ると、イヤになってしまいますよね。julia と一緒なら... まあ、大人は検算に使えますね。はたして、上記の記載が、受験生の助けになるのかは、とても不明です。
しかしながら、私個人の 「コンピューターって、何ができるのか? 」 という問いに答えがひとつ増えました。数値の四則に加えて、代数という抽象概念の理解も手伝ってくれますね。高校生の時に、これができたら、もっと、賢くなれたでしょうか。


